A function is a rule that, for every element associates an element The element is sometimes called the image of and the subset of consisting of images of elements in is called the image of That is,
Let be a function. Then is injective if distinct elements of are mapped to distinct elements of
That is, if and are in such that , then .
This is equivalent to saying if , then .
A synonym for "injective" is "one-to-one."
The function defined by is injective: if dividing both sides by yields
The function defined by is not injective; for example, but
The function defined by is injective; no two players were allowed to wear the same number.
The existence of an injective function gives information about the relative sizes of its domain and range:
If and are finite sets and is injective, then
None of the above
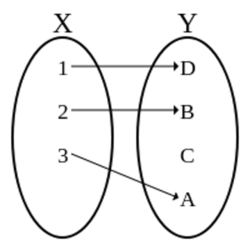
Let be a one-to-one (Injective) function with domain and range It is given that only one of the following statement is true and the remaining statements are false:
Find
Let be a function. Then is surjective if every element of is the image of at least one element of That is,
Symbolically,
A synonym for "surjective" is "onto."
The function defined by is not surjective: there is no integer such that because has no solutions in So is not in the image of
The function defined by is surjective. For any integer note that so is in the image of So the image of equals
The function defined by is surjective; every state has at least one senator.
The existence of a surjective function gives information about the relative sizes of its domain and range:
If and are finite sets and is surjective, then
Let and Then what is the number of onto functions from to
A function is bijective for two sets if every element of one set is paired with only one element of a second set, and each element of the second set is paired with only one element of the first set. This means that all elements are paired and paired once.
Let be a function. Then is bijective if it is injective and surjective; that is, every element is the image of exactly one element
The function defined by is a bijection.
The function defined by is a bijection.
The function defined by is a bijection.
Note that the above discussions imply the following fact (see the Bijective Functions wiki for examples):
If and are finite sets and is bijective, then
The following alternate characterization of bijections is often useful in proofs:
Suppose is nonempty. Then is a bijection if and only if there is a function such that is the identity on and is the identity on that is, and for all When this happens, the function is called the inverse function of and is also a bijection.
Show that the function defined by is a bijection.
Rather than showing is injective and surjective, it is easier to define by and to show that is the inverse of This follows from the identities Followup question: the same proof does not work for Why not?
rockwellefolotervis.blogspot.com
Source: https://brilliant.org/wiki/bijection-injection-and-surjection/

0 Response to "Injective but No Continuous Right Inverse"
Post a Comment