Python if a Function Fails Call Itself Again

Utilize of functions that call themselves

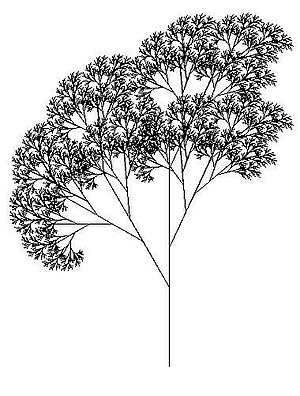
Tree created using the Logo programming language and relying heavily on recursion. Each branch tin be seen as a smaller version of a tree.

In informatics, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the aforementioned problem.^[1] Recursion solves such recursive problems by using functions that phone call themselves from within their own code. The arroyo can be applied to many types of issues, and recursion is one of the central ideas of information science.^[2]

The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite argument. In the same fashion, an space number of computations tin be described past a finite recursive program, fifty-fifty if this program contains no explicit repetitions.

—Niklaus Wirth, Algorithms + Information Structures = Programs, 1976^[3]

Most calculator programming languages support recursion by allowing a function to call itself from inside its ain code. Some functional programming languages (for instance, Clojure)^[4] practice not define any looping constructs but rely solely on recursion to repeatedly call code. Information technology is proved in computability theory that these recursive-merely languages are Turing complete; this means that they are as powerful (they can be used to solve the same problems) as imperative languages based on control structures such as while and for.

Repeatedly calling a part from within itself may cause the call stack to have a size equal to the sum of the input sizes of all involved calls. Information technology follows that, for problems that tin be solved hands by iteration, recursion is more often than not less efficient, and, for large problems, it is fundamental to use optimization techniques such equally tail call optimization.^{[ commendation needed ]}

Recursive functions and algorithms [edit]

A mutual algorithm design tactic is to divide a problem into sub-problems of the same blazon every bit the original, solve those sub-bug, and combine the results. This is often referred to as the dissever-and-conquer method; when combined with a lookup table that stores the results of previously solved sub-bug (to avoid solving them repeatedly and incurring extra computation time), it can exist referred to as dynamic programming or memoization.

Base case [edit]

A recursive role definition has one or more base cases, meaning input(s) for which the role produces a outcome trivially (without recurring), and one or more recursive cases, significant input(due south) for which the program recurs (calls itself). For example, the factorial function can exist defined recursively by the equations 0! = i and, for all due north > 0, n! = n(northward − one)!. Neither equation by itself constitutes a complete definition; the first is the base instance, and the 2d is the recursive example. Because the base of operations case breaks the concatenation of recursion, it is sometimes as well called the "terminating example".

The chore of the recursive cases can be seen as breaking downward complex inputs into simpler ones. In a properly designed recursive function, with each recursive telephone call, the input problem must be simplified in such a mode that eventually the base case must be reached. (Functions that are not intended to terminate under normal circumstances—for instance, some system and server processes—are an exception to this.) Neglecting to write a base of operations case, or testing for information technology incorrectly, can cause an infinite loop.

For some functions (such as one that computes the series for eastward = 1/0! + 1/1! + 1/two! + 1/3! + ...) in that location is non an obvious base of operations case implied by the input data; for these 1 may add a parameter (such as the number of terms to be added, in our series example) to provide a 'stopping criterion' that establishes the base case. Such an case is more naturally treated past corecursion,^{[ how? ]} where successive terms in the output are the fractional sums; this can be converted to a recursion by using the indexing parameter to say "compute the northwardth term (nth partial sum)".

Recursive data types [edit]

Many computer programs must process or generate an arbitrarily large quantity of data. Recursion is a technique for representing information whose verbal size is unknown to the programmer: the programmer tin can specify this information with a self-referential definition. There are 2 types of self-referential definitions: inductive and coinductive definitions.

Inductively divers information [edit]

An inductively defined recursive data definition is i that specifies how to construct instances of the data. For example, linked lists tin can exist divers inductively (here, using Haskell syntax):

                        data            ListOfStrings            =            EmptyList            |            Cons            String            ListOfStrings          

The code to a higher place specifies a listing of strings to be either empty, or a construction that contains a string and a listing of strings. The self-reference in the definition permits the construction of lists of any (finite) number of strings.

Another example of inductive definition is the natural numbers (or positive integers):

A natural number is either 1 or n+1, where northward is a natural number.

Similarly recursive definitions are oft used to model the construction of expressions and statements in programming languages. Language designers oftentimes express grammars in a syntax such as Backus–Naur course; here is such a grammar, for a simple language of arithmetic expressions with multiplication and improver:

                        <            expr            >            ::=            <            number            >            | (<            expr            >            *            <            expr            >)           | (<            expr            >            +            <            expr            >)          

This says that an expression is either a number, a product of two expressions, or a sum of ii expressions. By recursively referring to expressions in the second and tertiary lines, the grammer permits arbitrarily complicated arithmetic expressions such as (5 * ((3 * 6) + 8)), with more than than one product or sum operation in a single expression.

Coinductively defined data and corecursion [edit]

A coinductive data definition is i that specifies the operations that may exist performed on a slice of data; typically, cocky-referential coinductive definitions are used for data structures of infinite size.

A coinductive definition of infinite streams of strings, given informally, might await like this:

A stream of strings is an object s such that:  head(s) is a string, and  tail(s) is a stream of strings.        

This is very similar to an inductive definition of lists of strings; the deviation is that this definition specifies how to access the contents of the data structure—namely, via the accessor functions head and tail—and what those contents may be, whereas the inductive definition specifies how to create the structure and what information technology may be created from.

Corecursion is related to coinduction, and can be used to compute particular instances of (peradventure) space objects. As a programming technique, information technology is used most often in the context of lazy programming languages, and can exist preferable to recursion when the desired size or precision of a program'due south output is unknown. In such cases the program requires both a definition for an infinitely large (or infinitely precise) result, and a mechanism for taking a finite portion of that result. The problem of computing the first due north prime numbers is one that can be solved with a corecursive program (e.g. hither).

Types of recursion [edit]

Single recursion and multiple recursion [edit]

Recursion that contains only a single self-reference is known every bit single recursion , while recursion that contains multiple self-references is known every bit multiple recursion . Standard examples of single recursion include list traversal, such equally in a linear search, or computing the factorial function, while standard examples of multiple recursion include tree traversal, such every bit in a depth-first search.

Single recursion is often much more than efficient than multiple recursion, and can by and large be replaced by an iterative computation, running in linear time and requiring constant space. Multiple recursion, past dissimilarity, may require exponential time and space, and is more fundamentally recursive, not beingness able to exist replaced past iteration without an explicit stack.

Multiple recursion can sometimes be converted to unmarried recursion (and, if desired, thence to iteration). For case, while computing the Fibonacci sequence naively entails multiple iteration, equally each value requires two previous values, it can exist computed by unmarried recursion by passing 2 successive values every bit parameters. This is more naturally framed every bit corecursion, building upward from the initial values, while tracking two successive values at each step – see corecursion: examples. A more sophisticated case involves using a threaded binary tree, which allows iterative tree traversal, rather than multiple recursion.

Indirect recursion [edit]

Most basic examples of recursion, and nearly of the examples presented here, demonstrate straight recursion, in which a part calls itself. Indirect recursion occurs when a office is called not by itself only by another function that it called (either directly or indirectly). For case, if f calls f, that is direct recursion, but if f calls g which calls f, then that is indirect recursion of f. Chains of three or more functions are possible; for example, office one calls function 2, part 2 calls function 3, and function 3 calls function i over again.

Indirect recursion is also called mutual recursion, which is a more symmetric term, though this is simply a difference of emphasis, non a different notion. That is, if f calls g and and then k calls f, which in turn calls g again, from the point of view of f solitary, f is indirectly recursing, while from the point of view of one thousand alone, it is indirectly recursing, while from the betoken of view of both, f and grand are mutually recursing on each other. Similarly a set of 3 or more functions that telephone call each other can be called a prepare of mutually recursive functions.

Anonymous recursion [edit]

Recursion is usually done by explicitly calling a role by name. However, recursion can also be washed via implicitly calling a function based on the current context, which is particularly useful for bearding functions, and is known equally bearding recursion.

Structural versus generative recursion [edit]

Some authors classify recursion equally either "structural" or "generative". The stardom is related to where a recursive procedure gets the data that it works on, and how it processes that data:

[Functions that consume structured data] typically decompose their arguments into their immediate structural components and so procedure those components. If one of the immediate components belongs to the same course of information as the input, the part is recursive. For that reason, nosotros refer to these functions as (STRUCTURALLY) RECURSIVE FUNCTIONS.

Thus, the defining characteristic of a structurally recursive function is that the argument to each recursive telephone call is the content of a field of the original input. Structural recursion includes nearly all tree traversals, including XML processing, binary tree cosmos and search, etc. By considering the algebraic construction of the natural numbers (that is, a natural number is either zero or the successor of a natural number), functions such as factorial may likewise exist regarded as structural recursion.

Generative recursion is the alternative:

Many well-known recursive algorithms generate an entirely new piece of data from the given data and recur on it. HtDP (How to Design Programs) refers to this kind as generative recursion. Examples of generative recursion include: gcd, quicksort, binary search, mergesort, Newton's method, fractals, and adaptive integration.

—Matthias Felleisen, Avant-garde Functional Programming, 2002^[6]

This stardom is important in proving termination of a function.

• All structurally recursive functions on finite (inductively defined) data structures can easily be shown to cease, via structural induction: intuitively, each recursive call receives a smaller piece of input information, until a base case is reached.
• Generatively recursive functions, in contrast, do non necessarily feed smaller input to their recursive calls, so proof of their termination is non necessarily as simple, and avoiding infinite loops requires greater care. These generatively recursive functions can often exist interpreted as corecursive functions – each footstep generates the new data, such as successive approximation in Newton'due south method – and terminating this corecursion requires that the data eventually satisfy some condition, which is not necessarily guaranteed.
• In terms of loop variants, structural recursion is when in that location is an obvious loop variant, namely size or complexity, which starts off finite and decreases at each recursive step.
• By dissimilarity, generative recursion is when there is non such an obvious loop variant, and termination depends on a part, such as "mistake of approximation" that does not necessarily decrease to nil, and thus termination is not guaranteed without further analysis.

Implementation problems [edit]

In actual implementation, rather than a pure recursive function (unmarried check for base instance, otherwise recursive pace), a number of modifications may be made, for purposes of clarity or efficiency. These include:

• Wrapper function (at top)
• Short-circuiting the base of operations instance, aka "Arm'southward-length recursion" (at lesser)
• Hybrid algorithm (at lesser) – switching to a different algorithm once information is small enough

On the ground of elegance, wrapper functions are more often than not approved, while short-circuiting the base case is frowned upon, especially in academia. Hybrid algorithms are frequently used for efficiency, to reduce the overhead of recursion in pocket-sized cases, and arm's-length recursion is a special case of this.

Wrapper function [edit]

A wrapper function is a function that is direct called but does non recurse itself, instead calling a separate auxiliary office which actually does the recursion.

Wrapper functions can be used to validate parameters (so the recursive function tin can skip these), perform initialization (classify memory, initialize variables), particularly for auxiliary variables such equally "level of recursion" or partial computations for memoization, and handle exceptions and errors. In languages that support nested functions, the auxiliary function can be nested inside the wrapper function and utilize a shared scope. In the absence of nested functions, auxiliary functions are instead a divide function, if possible individual (as they are not called directly), and data is shared with the wrapper function by using laissez passer-by-reference.

Short-circuiting the base instance [edit]

Factorial: ordinary vs. short-circuit

Ordinary recursion	Short-circuit recursion
int fac1 ( int northward ) { if ( northward <= 0 ) render 1 ; else return fac1 ( n -ane ) * north ; }	static int fac2 ( int due north ) { // assert(n >= two); if ( n == ii ) render ii ; else return fac2 ( n -1 ) * n ; } int fac2wrapper ( int north ) { if ( n <= 1 ) render ane ; else return fac2 ( n ); }

Short-circuiting the base of operations instance, also known as arm's-length recursion, consists of checking the base case before making a recursive call – i.eastward., checking if the next call will be the base case, instead of calling and so checking for the base case. Short-circuiting is particularly done for efficiency reasons, to avoid the overhead of a part call that immediately returns. Note that since the base case has already been checked for (immediately before the recursive step), it does not need to be checked for separately, only one does need to use a wrapper function for the instance when the overall recursion starts with the base case itself. For example, in the factorial function, properly the base of operations case is 0! = 1, while immediately returning 1 for 1! is a curt circuit, and may miss 0; this can be mitigated past a wrapper function. The box shows C lawmaking to shortcut factorial cases 0 and ane.

Brusk-circuiting is primarily a concern when many base cases are encountered, such every bit Goose egg pointers in a tree, which can exist linear in the number of role calls, hence meaning savings for O(north) algorithms; this is illustrated below for a depth-commencement search. Short-circuiting on a tree corresponds to considering a leafage (non-empty node with no children) equally the base example, rather than considering an empty node every bit the base case. If in that location is merely a single base case, such as in computing the factorial, curt-circuiting provides merely O(1) savings.

Conceptually, short-circuiting tin can exist considered to either have the aforementioned base case and recursive pace, checking the base case just before the recursion, or information technology tin can be considered to take a different base case (one stride removed from standard base case) and a more circuitous recursive step, namely "check valid and so recurse", equally in because leaf nodes rather than Null nodes as base of operations cases in a tree. Considering curt-circuiting has a more complicated flow, compared with the clear separation of base case and recursive pace in standard recursion, it is often considered poor mode, particularly in academia.^[seven]

Depth-first search [edit]

A basic case of short-circuiting is given in depth-first search (DFS) of a binary tree; meet binary trees department for standard recursive discussion.

The standard recursive algorithm for a DFS is:

• base case: If current node is Zilch, return false
• recursive step: otherwise, check value of current node, return true if match, otherwise recurse on children

In short-circuiting, this is instead:

• check value of current node, return true if match,
• otherwise, on children, if non Null, and so recurse.

In terms of the standard steps, this moves the base instance check before the recursive step. Alternatively, these tin exist considered a different form of base case and recursive pace, respectively. Note that this requires a wrapper part to handle the case when the tree itself is empty (root node is Nil).

In the instance of a perfect binary tree of height h, there are 2 ^h+1−1 nodes and 2 ^h+1 Null pointers as children (2 for each of the 2 ^h leaves), so short-circuiting cuts the number of role calls in half in the worst case.

In C, the standard recursive algorithm may be implemented every bit:

                        bool                                    tree_contains            (            struct            node                                    *            tree_node            ,                                    int                                    i            )                                    {                                                if                                    (            tree_node                                    ==                                    NULL            )                                                render                                    fake            ;                                    // base case                                    else                                    if                                    (            tree_node            ->            data                                    ==                                    i            )                                                return                                    truthful            ;                                                else                                                return                                    tree_contains            (            tree_node            ->            left            ,                                    i            )                                    ||                                                tree_contains            (            tree_node            ->            right            ,                                    i            );                        }                      

The short-circuited algorithm may exist implemented as:

                        // Wrapper role to handle empty tree            bool                                    tree_contains            (            struct            node                                    *            tree_node            ,                                    int                                    i            )                                    {                                                if                                    (            tree_node                                    ==                                    Zippo            )                                                render                                    fake            ;                                    // empty tree                                    else                                                return                                    tree_contains_do            (            tree_node            ,                                    i            );                                    // telephone call auxiliary function            }                        // Assumes tree_node != NULL            bool                                    tree_contains_do            (            struct            node                                    *            tree_node            ,                                    int                                    i            )                                    {                                                if                                    (            tree_node            ->            data                                    ==                                    i            )                                                return                                    true            ;                                    // institute                                    else                                    // recurse                                    render                                    (            tree_node            ->            left                                    &&                                    tree_contains_do            (            tree_node            ->            left            ,                                    i            ))                                    ||                                                (            tree_node            ->            correct                                    &&                                    tree_contains_do            (            tree_node            ->            correct            ,                                    i            ));                        }                      

Notation the use of short-circuit evaluation of the Boolean && (AND) operators, so that the recursive call is made simply if the node is valid (non-Null). Note that while the beginning term in the AND is a arrow to a node, the second term is a boolean, so the overall expression evaluates to a boolean. This is a common idiom in recursive brusque-circuiting. This is in improver to the short-excursion evaluation of the Boolean || (OR) operator, to only bank check the correct child if the left child fails. In fact, the entire control flow of these functions can exist replaced with a single Boolean expression in a return statement, but legibility suffers at no do good to efficiency.

Hybrid algorithm [edit]

Recursive algorithms are oft inefficient for modest data, due to the overhead of repeated function calls and returns. For this reason efficient implementations of recursive algorithms oftentimes start with the recursive algorithm, only then switch to a different algorithm when the input becomes small. An important instance is merge sort, which is often implemented by switching to the non-recursive insertion sort when the information is sufficiently small, as in the tiled merge sort. Hybrid recursive algorithms can often exist further refined, as in Timsort, derived from a hybrid merge sort/insertion sort.

Recursion versus iteration [edit]

Recursion and iteration are every bit expressive: recursion can be replaced by iteration with an explicit call stack, while iteration can be replaced with tail recursion. Which approach is preferable depends on the trouble under consideration and the linguistic communication used. In imperative programming, iteration is preferred, peculiarly for uncomplicated recursion, equally it avoids the overhead of function calls and telephone call stack management, but recursion is generally used for multiple recursion. By contrast, in functional languages recursion is preferred, with tail recursion optimization leading to little overhead. Implementing an algorithm using iteration may not be easily achievable.

Compare the templates to compute 10_northward defined past x_{due north} = f(due north, ten_n-1) from ten_base:

part recursive(northward) if due north == base render tenbase else render f(north, recursive(n-1))

function iterative(n) x = xbase for i = base+1 to n 10 = f(i, x) render 10

For imperative language the overhead is to define the role, for functional language the overhead is to ascertain the accumulator variable 10.

For example, a factorial function may be implemented iteratively in C past assigning to a loop index variable and accumulator variable, rather than past passing arguments and returning values by recursion:

                        unsigned                                    int                                    factorial            (            unsigned                                    int                                    n            )                                    {                                                unsigned                                    int                                    product                                    =                                    1            ;                                    // empty product is i                                    while                                    (            due north            )                                    {                                                production                                    *=                                    n            ;                                                --            n            ;                                                }                                                return                                    product            ;                        }                      

Expressive ability [edit]

Nigh programming languages in apply today permit the direct specification of recursive functions and procedures. When such a office is called, the plan's runtime environment keeps rails of the various instances of the function (often using a phone call stack, although other methods may be used). Every recursive office tin can be transformed into an iterative function by replacing recursive calls with iterative control constructs and simulating the call stack with a stack explicitly managed by the programme.^{[8] [nine]}

Conversely, all iterative functions and procedures that tin can be evaluated by a computer (see Turing completeness) can exist expressed in terms of recursive functions; iterative control constructs such as while loops and for loops are routinely rewritten in recursive form in functional languages.^{[10] [11]} However, in practise this rewriting depends on tail call elimination, which is not a feature of all languages. C, Java, and Python are notable mainstream languages in which all function calls, including tail calls, may crusade stack allocation that would not occur with the employ of looping constructs; in these languages, a working iterative plan rewritten in recursive form may overflow the telephone call stack, although tail call emptying may be a feature that is not covered by a language's specification, and different implementations of the same linguistic communication may differ in tail call elimination capabilities.

Operation issues [edit]

In languages (such as C and Coffee) that favor iterative looping constructs, there is commonly significant time and infinite price associated with recursive programs, due to the overhead required to manage the stack and the relative slowness of part calls; in functional languages, a function call (peculiarly a tail telephone call) is typically a very fast operation, and the difference is unremarkably less noticeable.

As a concrete example, the divergence in performance between recursive and iterative implementations of the "factorial" example above depends highly on the compiler used. In languages where looping constructs are preferred, the iterative version may be equally much as several orders of magnitude faster than the recursive ane. In functional languages, the overall time divergence of the two implementations may exist negligible; in fact, the cost of multiplying the larger numbers get-go rather than the smaller numbers (which the iterative version given here happens to do) may overwhelm whatever fourth dimension saved by choosing iteration.

Stack space [edit]

In some programming languages, the maximum size of the telephone call stack is much less than the space available in the heap, and recursive algorithms tend to require more stack space than iterative algorithms. Consequently, these languages sometimes place a limit on the depth of recursion to avert stack overflows; Python is ane such language.^[12] Note the caveat beneath regarding the special case of tail recursion.

Vulnerability [edit]

Because recursive algorithms can be subject to stack overflows, they may exist vulnerable to pathological or malicious input.^[13] Some malware specifically targets a program's call stack and takes reward of the stack'south inherently recursive nature.^[14] Even in the absenteeism of malware, a stack overflow caused by unbounded recursion can be fatal to the program, and exception handling logic may not forbid the respective process from being terminated.^[15]

Multiply recursive issues [edit]

Multiply recursive issues are inherently recursive, because of prior state they need to track. One example is tree traversal as in depth-first search; though both recursive and iterative methods are used,^[xvi] they contrast with list traversal and linear search in a list, which is a singly recursive and thus naturally iterative method. Other examples include divide-and-conquer algorithms such every bit Quicksort, and functions such as the Ackermann function. All of these algorithms tin be implemented iteratively with the help of an explicit stack, merely the developer effort involved in managing the stack, and the complication of the resulting program, arguably outweigh whatsoever advantages of the iterative solution.

Refactoring recursion [edit]

Recursive algorithms can be replaced with non-recursive counterparts.^[17] One method for replacing recursive algorithms is to simulate them using heap memory in place of stack retention.^[18] An alternative is to develop a replacement algorithm entirely based on non-recursive methods, which can be challenging.^[xix] For example, recursive algorithms for matching wildcards, such as Rich Salz' wildmat algorithm,^[20] were once typical. Non-recursive algorithms for the same purpose, such as the Krauss matching wildcards algorithm, have been developed to avoid the drawbacks of recursion^[21] and have improved only gradually based on techniques such as collecting tests and profiling functioning.^[22]

Tail-recursive functions [edit]

Tail-recursive functions are functions in which all recursive calls are tail calls and hence do not build upwardly any deferred operations. For instance, the gcd function (shown over again below) is tail-recursive. In contrast, the factorial function (also below) is not tail-recursive; because its recursive phone call is not in tail position, information technology builds up deferred multiplication operations that must be performed after the terminal recursive telephone call completes. With a compiler or interpreter that treats tail-recursive calls every bit jumps rather than function calls, a tail-recursive part such equally gcd will execute using abiding space. Thus the program is essentially iterative, equivalent to using imperative language control structures like the "for" and "while" loops.

Tail recursion:	Augmenting recursion:
//INPUT: Integers x, y such that x >= y and y >= 0 int gcd ( int ten , int y ) { if ( y == 0 ) render x ; else return gcd ( y , x % y ); }	//INPUT: northward is an Integer such that n >= 0 int fact ( int n ) { if ( n == 0 ) return 1 ; else return northward * fact ( due north - one ); }

The significance of tail recursion is that when making a tail-recursive call (or whatsoever tail telephone call), the caller's render position demand not be saved on the telephone call stack; when the recursive telephone call returns, it volition branch direct on the previously saved return position. Therefore, in languages that recognize this property of tail calls, tail recursion saves both space and time.

Order of execution [edit]

Consider these 2 functions:

Function one [edit]

                        void                                    recursiveFunction            (            int                                    num            )                                    {                                                printf            (            "%d            \due north            "            ,                                    num            );                                                if                                    (            num                                    <                                    four            )                                                recursiveFunction            (            num                                    +                                    1            );                        }                      

Role two [edit]

                        void                                    recursiveFunction            (            int                                    num            )                                    {                                                if                                    (            num                                    <                                    four            )                                                recursiveFunction            (            num                                    +                                    1            );                                                printf            (            "%d            \n            "            ,                                    num            );                        }                      

Role 2 is part 1 with the lines swapped.

In the case of a role calling itself only in one case, instructions placed before the recursive telephone call are executed once per recursion before any of the instructions placed afterward the recursive call. The latter are executed repeatedly after the maximum recursion has been reached.

As well notation that the order of the print statements is reversed, which is due to the way the functions and statements are stored on the call stack.

Recursive procedures [edit]

Factorial [edit]

A classic example of a recursive procedure is the office used to calculate the factorial of a natural number:

${\displaystyle \operatorname {fact} (n)={\brainstorm{cases}1&{\mbox{if }}n=0\\northward\cdot \operatorname {fact} (n-1)&{\mbox{if }}n>0\\\end{cases}}}$

Pseudocode (recursive):
function factorial is: input: integer n such that n >= 0 output: [northward × (n-1) × (n-two) × ... × 1] 1. if n is 0, render 1 2. otherwise, return [ n × factorial(n-one) ] finish factorial

The function can also be written as a recurrence relation:

${\displaystyle b_{due north}=nb_{n-i}}$

${\displaystyle b_{0}=ane}$

This evaluation of the recurrence relation demonstrates the computation that would be performed in evaluating the pseudocode above:

Calculating the recurrence relation for n = 4:
b4 = four × b3 = 4 × (3 × bii) = 4 × (3 × (2 × b1)) = four × (3 × (2 × (1 × b0))) = 4 × (three × (2 × (1 × 1))) = four × (3 × (2 × 1)) = 4 × (3 × 2) = four × half dozen = 24

This factorial function tin also be described without using recursion by making utilise of the typical looping constructs found in imperative programming languages:

Pseudocode (iterative):
office factorial is: input: integer n such that n >= 0 output: [n × (due north-1) × (n-two) × ... × ane] 1. create new variable called running_total with a value of one 2. begin loop 1. if due north is 0, exit loop 2. set running_total to (running_total × north) 3. decrement n iv. repeat loop three. render running_total end factorial

The imperative code above is equivalent to this mathematical definition using an accumulator variable t :

${\displaystyle {\begin{aligned}\operatorname {fact} (due north)&=\operatorname {fact_{acc}} (n,1)\\\operatorname {fact_{acc}} (north,t)&={\begin{cases}t&{\mbox{if }}due north=0\\\operatorname {fact_{acc}} (due north-1,nt)&{\mbox{if }}n>0\\\cease{cases}}\finish{aligned}}}$

The definition in a higher place translates straightforwardly to functional programming languages such as Scheme; this is an example of iteration implemented recursively.

Greatest common divisor [edit]

The Euclidean algorithm, which computes the greatest mutual divisor of two integers, can be written recursively.

Function definition:

${\displaystyle \gcd(x,y)={\brainstorm{cases}x&{\mbox{if }}y=0\\\gcd(y,\operatorname {remainder} (x,y))&{\mbox{if }}y>0\\\cease{cases}}}$

Pseudocode (recursive):
function gcd is: input: integer x, integer y such that 10 > 0 and y >= 0 1. if y is 0, return x 2. otherwise, render [ gcd( y, (remainder of x/y) ) ] stop gcd

Recurrence relation for greatest common divisor, where ${\displaystyle x\%y}$ expresses the residual of ${\displaystyle 10/y}$ :

${\displaystyle \gcd(x,y)=\gcd(y,x\%y)}$ if ${\displaystyle y\neq 0}$

${\displaystyle \gcd(x,0)=ten}$

Computing the recurrence relation for x = 27 and y = nine:
gcd(27, 9) = gcd(9, 27 % 9) = gcd(ix, 0) = ix
Calculating the recurrence relation for ten = 111 and y = 259:
gcd(111, 259) = gcd(259, 111 % 259) = gcd(259, 111) = gcd(111, 259 % 111) = gcd(111, 37) = gcd(37, 111 % 37) = gcd(37, 0) = 37

The recursive program above is tail-recursive; it is equivalent to an iterative algorithm, and the computation shown above shows the steps of evaluation that would be performed by a language that eliminates tail calls. Beneath is a version of the same algorithm using explicit iteration, suitable for a language that does non eliminate tail calls. By maintaining its country entirely in the variables 10 and y and using a looping construct, the plan avoids making recursive calls and growing the call stack.

Pseudocode (iterative):
part gcd is: input: integer x, integer y such that x >= y and y >= 0 1. create new variable chosen remainder 2. begin loop 1. if y is nada, exit loop ii. set remainder to the remainder of 10/y three. set x to y 4. fix y to residual 5. repeat loop 3. render x end gcd

The iterative algorithm requires a temporary variable, and even given noesis of the Euclidean algorithm it is more difficult to empathise the process past unproblematic inspection, although the ii algorithms are very similar in their steps.

Towers of Hanoi [edit]

The Towers of Hanoi is a mathematical puzzle whose solution illustrates recursion.^{[23] [24]} There are three pegs which can agree stacks of disks of different diameters. A larger disk may never be stacked on peak of a smaller. Starting with north disks on one peg, they must exist moved to another peg ane at a time. What is the smallest number of steps to move the stack?

Function definition:

${\displaystyle \operatorname {hanoi} (due north)={\begin{cases}1&{\mbox{if }}due north=1\\2\cdot \operatorname {hanoi} (n-1)+1&{\mbox{if }}n>1\\\terminate{cases}}}$

Recurrence relation for hanoi:

${\displaystyle h_{n}=2h_{n-1}+ane}$

${\displaystyle h_{i}=1}$

Computing the recurrence relation for n = 4:
hanoi(iv) = two×hanoi(iii) + one = 2×(2×hanoi(two) + 1) + i = ii×(2×(2×hanoi(i) + one) + i) + 1 = 2×(2×(2×1 + ane) + 1) + 1 = 2×(2×(3) + 1) + 1 = 2×(7) + ane = 15

Example implementations:

Pseudocode (recursive):
function hanoi is: input: integer n, such that due north >= one 1. if n is ane then return i 2. render [2 * [phone call hanoi(n-1)] + one] end hanoi

Although not all recursive functions take an explicit solution, the Tower of Hanoi sequence can be reduced to an explicit formula.^[25]

An explicit formula for Towers of Hanoi:
h1 = 1 = two1 - one h2 = 3 = 22 - i hiii = 7 = 23 - 1 h4 = 15 = two4 - 1 h5 = 31 = 25 - 1 h6 = 63 = 2half dozen - 1 h7 = 127 = 27 - 1 In general: hn = 2n - ane, for all north >= one

Binary search [edit]

The binary search algorithm is a method of searching a sorted array for a single chemical element by cutting the array in half with each recursive pass. The trick is to selection a midpoint near the center of the array, compare the data at that point with the data beingness searched and so responding to ane of three possible conditions: the data is found at the midpoint, the data at the midpoint is greater than the information being searched for, or the data at the midpoint is less than the data being searched for.

Recursion is used in this algorithm because with each pass a new array is created past cutting the old one in one-half. The binary search procedure is then chosen recursively, this time on the new (and smaller) array. Typically the assortment's size is adjusted by manipulating a beginning and ending index. The algorithm exhibits a logarithmic order of growth because it substantially divides the trouble domain in half with each laissez passer.

Example implementation of binary search in C:

                                                /*                          Telephone call binary_search with proper initial atmospheric condition.                          INPUT:                          data is an array of integers SORTED in ASCENDING order,                          toFind is the integer to search for,                          count is the total number of elements in the array                          OUTPUT:                          result of binary_search                          */                                                int                                    search            (            int                                    *            data            ,                                    int                                    toFind            ,                                    int                                    count            )                                                {                                                //  Outset = 0 (beginning index)                                    //  Terminate = count - i (top index)                                    render                                    binary_search            (            data            ,                                    toFind            ,                                    0            ,                                    count            -1            );                                                }                                                /*                          Binary Search Algorithm.                          INPUT:                          data is a array of integers SORTED in ASCENDING lodge,                          toFind is the integer to search for,                          get-go is the minimum array index,                          cease is the maximum array index                          OUTPUT:                          position of the integer toFind inside array data,                          -one if not establish                          */                                                int                                    binary_search            (            int                                    *            data            ,                                    int                                    toFind            ,                                    int                                    start            ,                                    int                                    cease            )                                                {                                                //Get the midpoint.                                    int                                    mid                                    =                                    beginning                                    +                                    (            end                                    -                                    start            )            /            2            ;                                    //Integer partition                                    if                                    (            kickoff                                    >                                    end            )                                    //Terminate status (base of operations case)                                    return                                    -ane            ;                                                else                                    if                                    (            data            [            mid            ]                                    ==                                    toFind            )                                    //Plant, render index                                    return                                    mid            ;                                                else                                    if                                    (            data            [            mid            ]                                    >                                    toFind            )                                    //Data is greater than toFind, search lower half                                    render                                    binary_search            (            information            ,                                    toFind            ,                                    first            ,                                    mid            -i            );                                                else                                    //Data is less than toFind, search upper half                                    return                                    binary_search            (            information            ,                                    toFind            ,                                    mid            +            1            ,                                    stop            );                                                }                      

Recursive data structures (structural recursion) [edit]

An of import application of recursion in informatics is in defining dynamic data structures such as lists and trees. Recursive data structures tin can dynamically grow to a theoretically space size in response to runtime requirements; in dissimilarity, the size of a static array must be set at compile time.

"Recursive algorithms are especially appropriate when the underlying problem or the data to be treated are defined in recursive terms."^[26]

The examples in this section illustrate what is known every bit "structural recursion". This term refers to the fact that the recursive procedures are interim on data that is defined recursively.

Every bit long as a programmer derives the template from a data definition, functions utilize structural recursion. That is, the recursions in a function'south torso consume some immediate piece of a given compound value.^[six]

Linked lists [edit]

Below is a C definition of a linked list node structure. Find specially how the node is defined in terms of itself. The "next" element of struct node is a pointer to another struct node, effectively creating a listing blazon.

                        struct            node                        {                                                int                                    data            ;                                    // some integer data                                    struct            node                                    *            next            ;                                    // arrow to another struct node            };                      

Because the struct node information structure is defined recursively, procedures that operate on it can be implemented naturally equally recursive procedures. The list_print procedure defined below walks downwardly the list until the list is empty (i.eastward., the list pointer has a value of NULL). For each node information technology prints the data element (an integer). In the C implementation, the listing remains unchanged past the list_print procedure.

                        void                                    list_print            (            struct            node                                    *            listing            )                        {                                                if                                    (            list                                    !=                                    NULL            )                                    // base of operations case                                    {                                                printf                                    (            "%d "            ,                                    list            ->            data            );                                    // print integer information followed past a space                                    list_print                                    (            listing            ->            adjacent            );                                    // recursive call on the adjacent node                                    }                        }                      

Binary trees [edit]

Beneath is a simple definition for a binary tree node. Like the node for linked lists, it is defined in terms of itself, recursively. There are two self-referential pointers: left (pointing to the left sub-tree) and right (pointing to the correct sub-tree).

                        struct            node                        {                                                int                                    data            ;                                    // some integer data                                    struct            node                                    *            left            ;                                    // arrow to the left subtree                                    struct            node                                    *            correct            ;                                    // indicate to the correct subtree            };                      

Operations on the tree can be implemented using recursion. Notation that because there are 2 self-referencing pointers (left and right), tree operations may require two recursive calls:

                        // Test if tree_node contains i; return 1 if then, 0 if not.            int                                    tree_contains            (            struct            node                                    *            tree_node            ,                                    int                                    i            )                                    {                                                if                                    (            tree_node                                    ==                                    Zilch            )                                                render                                    0            ;                                    // base case                                    else                                    if                                    (            tree_node            ->            data                                    ==                                    i            )                                                return                                    one            ;                                                else                                                return                                    tree_contains            (            tree_node            ->            left            ,                                    i            )                                    ||                                    tree_contains            (            tree_node            ->            right            ,                                    i            );                        }                      

At most ii recursive calls volition exist made for whatsoever given call to tree_contains equally defined higher up.

                        // Inorder traversal:            void                                    tree_print            (            struct            node                                    *            tree_node            )                                    {                                                if                                    (            tree_node                                    !=                                    Goose egg            )                                    {                                    // base case                                    tree_print            (            tree_node            ->            left            );                                    // go left                                    printf            (            "%d "            ,                                    tree_node            ->            information            );                                    // print the integer followed by a space                                    tree_print            (            tree_node            ->            right            );                                    // become right                                    }                        }                      

The above instance illustrates an in-order traversal of the binary tree. A Binary search tree is a special case of the binary tree where the data elements of each node are in order.

Filesystem traversal [edit]

Since the number of files in a filesystem may vary, recursion is the only practical way to traverse and thus enumerate its contents. Traversing a filesystem is very similar to that of tree traversal, therefore the concepts behind tree traversal are applicable to traversing a filesystem. More specifically, the code below would be an example of a preorder traversal of a filesystem.

                                    import            java.io.File            ;                                    public            form            FileSystem            {                                    public            static            void            main            (            String            []            args            )            {                        traverse            ();                        }                                    /**                                      * Obtains the filesystem roots                                      * Proceeds with the recursive filesystem traversal                                      */                        private            static            void            traverse            ()            {                        File            []            fs            =            File            .            listRoots            ();                        for            (            int            i            =            0            ;            i            <            fs            .            length            ;            i            ++            )            {                        System            .            out            .            println            (            fs            [            i            ]            );                        if            (            fs            [            i            ]            .            isDirectory            ()            &&            fs            [            i            ]            .            canRead            ())            {                        rtraverse            (            fs            [            i            ]            );                        }                        }                        }                                    /**                                      * Recursively traverse a given directory                                      *                                      * @param fd indicates the starting betoken of traversal                                      */                        private            static            void            rtraverse            (            File            fd            )            {                        File            []            fss            =            fd            .            listFiles            ();                                    for            (            int            i            =            0            ;            i            <            fss            .            length            ;            i            ++            )            {                        Organisation            .            out            .            println            (            fss            [            i            ]            );                        if            (            fss            [            i            ]            .            isDirectory            ()            &&            fss            [            i            ]            .            canRead            ())            {                        rtraverse            (            fss            [            i            ]            );                        }                        }                        }                                    }          

This code is both recursion and iteration - the files and directories are iterated, and each directory is opened recursively.

The "rtraverse" method is an example of direct recursion, whilst the "traverse" method is a wrapper part.

The "base case" scenario is that in that location will e'er exist a fixed number of files and/or directories in a given filesystem.

Fourth dimension-efficiency of recursive algorithms [edit]

The fourth dimension efficiency of recursive algorithms tin can be expressed in a recurrence relation of Big O notation. They tin can (usually) then be simplified into a single Big-O term.

Shortcut rule (chief theorem) [edit]

If the fourth dimension-complexity of the part is in the form

$${\displaystyle T(n)=a\cdot T(n/b)+f(n)}$$

Then the Large O of the time-complexity is thus:

where a represents the number of recursive calls at each level of recursion, b represents by what factor smaller the input is for the next level of recursion (i.e. the number of pieces you divide the problem into), and f(northward) represents the work that the function does independently of any recursion (e.g. sectionalization, recombining) at each level of recursion.

See also [edit]

• Functional programming
• Computational trouble
• Hierarchical and recursive queries in SQL
• Kleene–Rosser paradox
• Open recursion
• Recursion
• Sierpiński curve
• McCarthy 91 role
• μ-recursive functions
• Primitive recursive functions
• Tak (function)

Notes [edit]

1. ^ Graham, Ronald; Knuth, Donald; Patashnik, Oren (1990). "ane: Recurrent Issues". Concrete Mathematics. ISBN0-201-55802-5.
2. ^ Epp, Susanna (1995). Discrete Mathematics with Applications (2d ed.). p. 427. ISBN978-0-53494446-nine.
3. ^ Wirth, Niklaus (1976). Algorithms + Data Structures = Programs. Prentice-Hall. p. 126. ISBN978-0-13022418-7.
4. ^ "Functional Programming | Clojure for the Brave and True". world wide web.braveclojure.com . Retrieved 2020-10-21 .
5. ^ Felleisen et al. 2001, art V "Generative Recursion
6. ^ ^{a b} Felleisen, Matthias (2002). "Developing Interactive Spider web Programs". In Jeuring, Johan (ed.). Advanced Functional Programming: 4th International School (PDF). Springer. p. 108. ISBN9783540448334.
7. ^ Mongan, John; Giguère, Eric; Kindler, Noah (2013). Programming Interviews Exposed: Secrets to Landing Your Next Job (third ed.). Wiley. p. 115. ISBN978-1-118-26136-i.
8. ^ Hetland, Magnus Prevarication (2010), Python Algorithms: Mastering Basic Algorithms in the Python Language, Apress, p. 79, ISBN9781430232384 .
9. ^ Drozdek, Adam (2012), Data Structures and Algorithms in C++ (4th ed.), Cengage Learning, p. 197, ISBN9781285415017 .
10. ^ Shivers, Olin. "The Beefcake of a Loop - A story of scope and command" (PDF). Georgia Institute of Technology. Retrieved 2012-09-03 .
11. ^ Lambda the Ultimate. "The Anatomy of a Loop". Lambda the Ultimate. Retrieved 2012-09-03 .
12. ^ "27.1. sys — Organisation-specific parameters and functions — Python v2.7.3 documentation". Docs.python.org. Retrieved 2012-09-03 .
13. ^ Krauss, Kirk J. (2014). "Matching Wildcards: An Empirical Way to Tame an Algorithm". Dr. Dobb's Journal.
14. ^ Mueller, Oliver (2012). "Anatomy of a Stack Dandy Attack and How GCC Prevents It". Dr. Dobb'south Journal.
15. ^ "StackOverflowException Class". .NET Framework Course Library. Microsoft Developer Network. 2018.
16. ^ "Depth First Search (DFS): Iterative and Recursive Implementation". Techie Delight. 2018.
17. ^ Mitrovic, Ivan. "Replace Recursion with Iteration". ThoughtWorks.
18. ^ La, Woong Gyu (2015). "How to supercede recursive functions using stack and while-loop to avoid the stack-overflow". CodeProject.
19. ^ Moertel, Tom (2013). "Tricks of the trade: Recursion to Iteration, Part two: Eliminating Recursion with the Time-Traveling Secret Characteristic Trick".
20. ^ Salz, Rich (1991). "wildmat.c". GitHub.
21. ^ Krauss, Kirk J. (2008). "Matching Wildcards: An Algorithm". Dr. Dobb's Journal.
22. ^ Krauss, Kirk J. (2018). "Matching Wildcards: An Improved Algorithm for Big Information". Develop for Performance.
23. ^ Graham, Knuth & Patashnik 1990, §1.1: The Tower of Hanoi
24. ^ Epp 1995, pp. 427–430: The Belfry of Hanoi
25. ^ Epp 1995, pp. 447–448: An Explicit Formula for the Tower of Hanoi Sequence
26. ^ Wirth 1976, p. 127

References [edit]

• Barron, David William (1968) [1967]. Written at Cambridge, United kingdom of great britain and northern ireland. Gill, Stanley (ed.). Recursive techniques in programming. Macdonald Computer Monographs (one ed.). London, U.k.: Macdonald & Co. (Publishers) Ltd. SBN356-02201-3. (8+64 pages)
• Felleisen, Matthias; Findler, Robert B.; Flatt, Matthew; Krishnamurthi, Shriram (2001). How To Design Programs: An Introduction to Computing and Programming. MIT Press. ISBN0262062186.
• Rubio-Sanchez, Manuel (2017). Introduction to Recursive Programming. CRC Press. ISBN978-ane-351-64717-5.
• Pevac, Irena (2016). Practicing Recursion in Java. CreateSpace Independent. ISBN978-ane-5327-1227-ii.
• Roberts, Eric (2005). Thinking Recursively with Java. Wiley. ISBN978-0-47170146-0.
• Rohl, Jeffrey S. (1984). Recursion Via Pascal. Cambridge Academy Printing. ISBN978-0-521-26934-6.
• Helman, Paul; Veroff, Robert. Walls and Mirrors.
• Abelson, Harold; Sussman, Gerald Jay; Sussman, Julie (1996). Structure and Interpretation of Computer Programs (second ed.). MIT Printing. ISBN0-262-51087-one.
• Dijkstra, Edsger W. (1960). "Recursive Programming". Numerische Mathematik. ii (ane): 312–318. doi:ten.1007/BF01386232. S2CID 127891023.

rockwellefolotervis.blogspot.com

Source: https://en.wikipedia.org/wiki/Recursion_(computer_science)

Share this post